WEB TUTORIAL - Group Theory
| C2v | E | C2 (z) | Linear functions, rotations | Quadratic functions | Cubic functions | ||
| A1 | +1 | +1 | +1 | +1 | z | x2, y2, z2 | z3, x2z, y2z |
| A2 | +1 | +1 | -1 | -1 | Rz | xy | xyz |
| B1 | +1 | -1 | +1 | -1 | x, Ry | xz | xz2, x3, xy2 |
| B2 | +1 | -1 | -1 | +1 | y, Rx | yz | yz2, y3, x2y |
You must consider the bonds which have moved, and hence how many bonds remain unchanged after the symmetry element has been completed. Not the atoms!
E.g. C2 rotation:
One atom has stayed in the same position, but imagine the bonds are labelled 'A' and 'B'. Thus following around the pictures, you can see that bond 'A' and bond 'B' have changed positions, hence for C2 rotation there are NO Unchanged bonds.
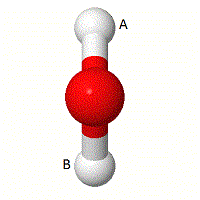
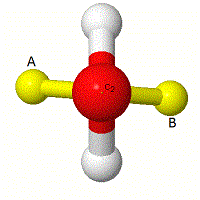
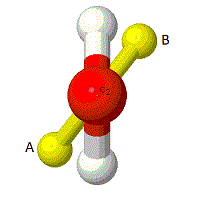
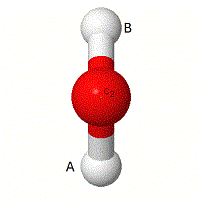
Consider each symmetry element in turn, and answer how many unchanged bonds there are in each case after the symmetry element has been completed and pick one of the following answers.
indicates the number of unchanged bonds for the C2 rotation and so forth.